Problema B. 5030, KöMaL mayo 2019

El siguiente problema fue propuesto por Paul Erdös.

Problema. Demuestre que todo entero mayor que $ 1$ puede ser representado como la suma de términos de la forma $ 2^p \cdot 3^q$ mayor que $ 1$, tales que ningún término en la suma es un divisor de otro término.

Antes de empezar con la resolución del problema, comenzemos escribiendo los siguientes números en la representación deseada:

\[\begin{eqnarray} 2 &=& 2^1 \cdot 3^0\\ 3 &=& 2^0 \cdot 3^1 \\ 4 &=& 2^2 \cdot 3^0 \\ 5 &=& 2^1 + 3^1 \\ 6 &=& 2 \cdot 3 \\ 7 &=& 3^1 + 2^2\\ 8 &=& 2^3 \cdot 3^0 \\ 9 &=& 2^0 \cdot 3^2 \\ 10 &=& 2 \cdot 5 = 2 \cdot (2 + 3) = 2^2 + 2\cdot 3 \\ 11 &=& 3^2 + 2 \\ 12 &=& 2^2 \cdot 3^1 \end{eqnarray}\]

De esta lista podemos observar que lo interesante ocurre con los números de la forma $ 2^p \cdot 3^q \cdot m$ con $ (m, 6) = 1 $ y $p, q$ enteros no negativos. Si descomponemos a $m$ en la forma deseada, entonces solo tenemos que multiplicar $ 2^p \cdot 3^q$ por esta descomposición y la proposición se satisface. Por tanto, hemos sustituido el problema original por uno equivalente: demostrar la propisición para los naturales $ m$ tales que $ (6, m) = 1$. Queda solo responder, ¿cómo podemos encontrar tal descomposición para estos números $ m$?

Solución. Consideremos los naturales $ n$ tales que $ (6, n) = 1$. Escribamos $ n = 3^{q_1} + 2^{p_1} \cdot m_1$, dónde $q_1$ es el natural más grande tal que $ n - 3^{q_1} > 0$ y $ (2, m_1) = 1$. Observe que esto siempre es posible ya que $n > 3$ y $ n - 3^{q_1}$ es par.

Ahora bien, si $ m_1 = 1$ acabamos. Si no, podemos repetir el proceso anterior para $ m_1$: escribamos $ m_1 = 3^{q_2} + 2^{p_2} m_2$ dónde $ q_2$ es el natural más grande tal que $ m_1 - 3^{q_2} > 0$ y $(2, m_2) = 1$. Además, por la definición de $q_1$, se comprueba que $q_1 > q_2$ ¹.

Podemos repetir el proceso anterior para $m_2$ y en general para $m_j$. Es claro que el proceso anterior termina, digamos en el $k-$ésimo paso. Por tanto obtenemos

\[\begin{eqnarray} n &=& 3^{q_1} + 2^{p_1} ( 3^{q_2} + 2^{p_2} (3^{q_3} +2^{p_3} ( \cdots + 2^{p_{k-1}} ( 3^{q_k} + 2^{p_k} ) ) \\ &=& 3^{q_1} + 2^{s_2} \cdot 3^{q_2} + 2^{s_3} \cdot 3^{q_3} + \cdots + 2^{s_{k}} \cdot 3^{q_{k}} + 2^{s_{k+1}}, \end{eqnarray}\]

con $ q_1 > q_2 > \cdots > q_k$ y $ s_r = \sum_{i < r}{p_i}$. Por definición $ s_j < s_l $ si $j < l$. Luego, cualquier sumando en la ecuación anterior no divide al resto.

Para el caso $(6, n) > 1$, hagamos $ n = 2^{p} \cdot 3^{q} \cdot m$ con $ (6, m) = 1$ y apliquemos a $m$ el resultado anterior.

Observación. Esta descomposición no es única: $19 = 3^2 + 2 \cdot 3 + 2^2 = 2^4 + 3$.

Probabilidad

Dado lo anterior, podemos preguntarnos ¿cuántos términos en la descomposición espero tener para un número dado?² Lo interesante de la demostración anterior es que nos ofrece un algoritmo que regresa la descomposición deseada. Tratando de contestar la pregunta, podemos generar la descomposición para todo número menor que un número $\alpha$, contar el número de términos y obtener las frecuencias. La siguiente tabla presenta estadísticos para $x \leq 10^n $, $n = 3, \ldots, 8$.

$x < 10^n$	Media	D. estándar	Mediana	Máximo
3	2.9949	0.9025	3.0	6
4	3.9203	1.0514	4.0	8
5	4.8549	1.1842	5.0	10
6	5.7879	1.2947	6.0	12
7	6.7183	1.4080	7.0	14

De la tabla observamos que tanto la mediana como la media son aproximadamente igual al exponente $n$. La desviación estándar, parece tener un comportamiento creciente conforme $n$ crece. El histograma que sigue indica que el comportamiento de esta variable se comporta bien.

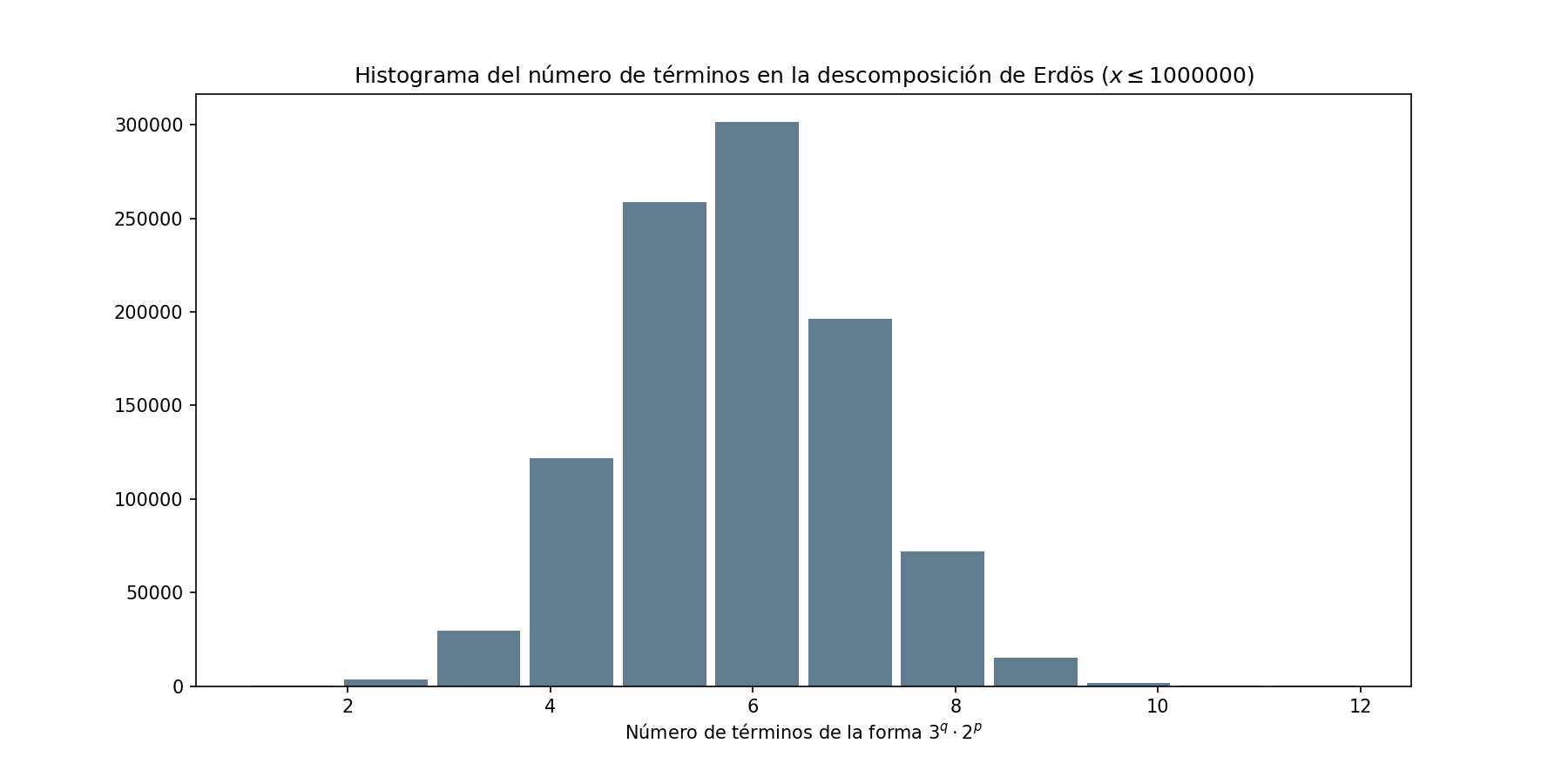
Aunque lo anterior son solo observaciones, parece ser que esta variable se comporta de manera gaussiana (o algo parecido).

El código de estos experimentos se pueden encontrar aquí. Ojo, el código no está optimizado.

---

Notas:

---