¿Por qué existen los huracanes?

Este post no trata sobre climatología ni meteorología. No, este post trata sobre uno de los teoremas más bonitos y profundos de la matemática: El Teorema de la Bola Peluda (TBP en adelante). Pero como todo resultado de esta categoría, el TBP tiene implicaciones en otras áreas del conocimiento aparentemente ajenas (the unreasonable effectiveness of mathematics in the natural sciences, como suele decirse). Así que no te preocupes, querido lector, también hablaremos sobre huracanes.

Cabe preguntarse, ¿por qué este teorema tiene este nombre tan peculiar? Bueno, en primer lugar, el TBP trata sobre esferas. Pero esferas en cualquier dimensión: uno, dos, cien o cuatro mil trescientos (elija su número favorito). En segundo lugar, trata sobre el comportamiento de campos vectoriales sobre estas esferas. La bola peluda es solo un caso particular de este teorema, siendo “bola”, una esfera de dimensión dos, y los “pelos” un campo de vectores sobre esta. La formulación formal del teorema es la siguiente.

 

Teorema. Existe un campo vectorial en $S^n$ que no se anula en ningún punto si y solo si $n$ es impar.

 

Desmenucemos los conceptos de este teorema. Una esfera de dimensión $n$, o dicho de manera simple la n-esfera, $S^n$ se define, para todo entero no negativo $n$, como

\[S^n = \{x \in \mathbb{R}^{n+1}: \lvert x \rvert = 1 \}.\]

Es decir, son los puntos en $\mathbb{R}^{n+1} $ que se encuentran a una distancia igual a 1 respecto al origen. Consideremos, para clarificar lo anterior, el caso $n = 0$. En este caso, la 0-esfera es el conjunto {-1, 1}, pues estos son los únicos puntos en la recta real que están a una distancia unitaria respecto al origen. De manera similar, se deduce que la 1-esfera es el círculo unitario en el plano y que la 2-esfera es una esfera en el espacio (como las de navidad).

El otro concepto central es el de “campo vectorial”. Un campo vectorial sobre la n-esfera es un mapeo continuo $V: S^n \rightarrow \mathbb{R}^{n+1}$, tal que $x$ y $V(x)$ son ortogonales. Intuitivamente, un campo vectorial asigna a cada punto de la n-esfera una flecha tangente, teniendo cuidado con que esta asignación sea continua. Un campo vectorial que no se anula, es simplemente aquel que su valor nunca es cero. De nuevo, uno puede imaginarse que el vector cero es una flecha que no tiene longitud ni apunta a ningún lado (¿qué?).

Entonces, ¿qué nos dice el TBP? Primero, este es un teorema de existencia: si la dimensión de la esfera es impar, podemos encontrar un campo vectorial que no se anula en ningún punto de la esfera. Pero también es un teorema de equivalencia: ¡Sólo las esferas de dimensión impar satisfacen lo anterior!

¿Qué tienen de especial las esferas impares respecto las pares? Bueno, realmente esto es un misterio qué aún en nuestros días no entendemos con totalidad. Tal vez hablemos de esto en otro post. Por ahora, considero que nos servirá trabajar con los siguientes ejemplos.

El círculo unitario $S^1$, es una esfera de dimensión impar. Por tanto, el TBP establece que podemos definir un campo vectorial en $S^1$ que no se anule en ningún punto. Existen muchos ejemplos sencillos de estos campos. Nosotros presentaremos uno cuya construcción se debe a otro concepto muy importante en las matemáticas: los grupos de Lie (del cual tal vez hablaré en otro post).

LLamemos $R$ a nuestro campo vectorial. En el punto $(1, 0)$ de $S^1$, este campo asigna el vector $(0, 1)$. Note que este vector satisface la condición de ortogonalidad (o perpendicularidad). Ahora, imaginemos que $S^1$ es el contorno de una rueda, cuyo eje de rotación se encuentra en el origen (el centro del círculo). Si imaginamos que la base del vector $(0,1)$ se encuentra en el punto $(1, 0)$ y hacemos rotar a la rueda en contra de las manecillas del reloj con una velocidad constante, veremos como la flecha se mueve continuamente al rededor de $S^1$. Este será nuestro campo vectorial $R$. Vea la siguiente figura para una explicación gráfica.

Si asumimos que ya hicimos la talacha de encontrar las ecuaciones, concluiríamos que el campo $R$ está definido como $R(x, y) = (-y, x)$. Claro que este campo es continuo y además por construcción (y como podemos ver en la fórmulita) nunca se anula en los puntos de la 1-esfera.

Ahora pasemos al caso de la bola peluda, es decir, el caso de un campo vectorial definido en la 2-esfera. Uno podría pensar que la construcción anterior funciona: ponemos una flecha en un punto de la pelota y la empezamos a rotar hasta cubrir toda la superficie con flechas. Rápidamente veríamos que si hacemos esto, aparecerían “apartados” o “remolinos” en la cabellera de flechas. Estos son los puntos donde el campo vectorial se anula.

Tal vez uno podría pensar que lo anterior es solo un caso aislado. Lo invito a que pruebe con sus campos favoritos. Se dará cuenta que, o bien sus funciones no son continuas, o bien siempre existe un punto en el que el campo se anula. En su excelente libro, Topology from the differentiable viewpoint, John Milnor nos muestra algunos bocetos de campos vectoriales sobre la 2-esfera con distintos tipos de “remolinos” (donde el campo vectorial se anula). Estos se muestran en la siguiente figura.

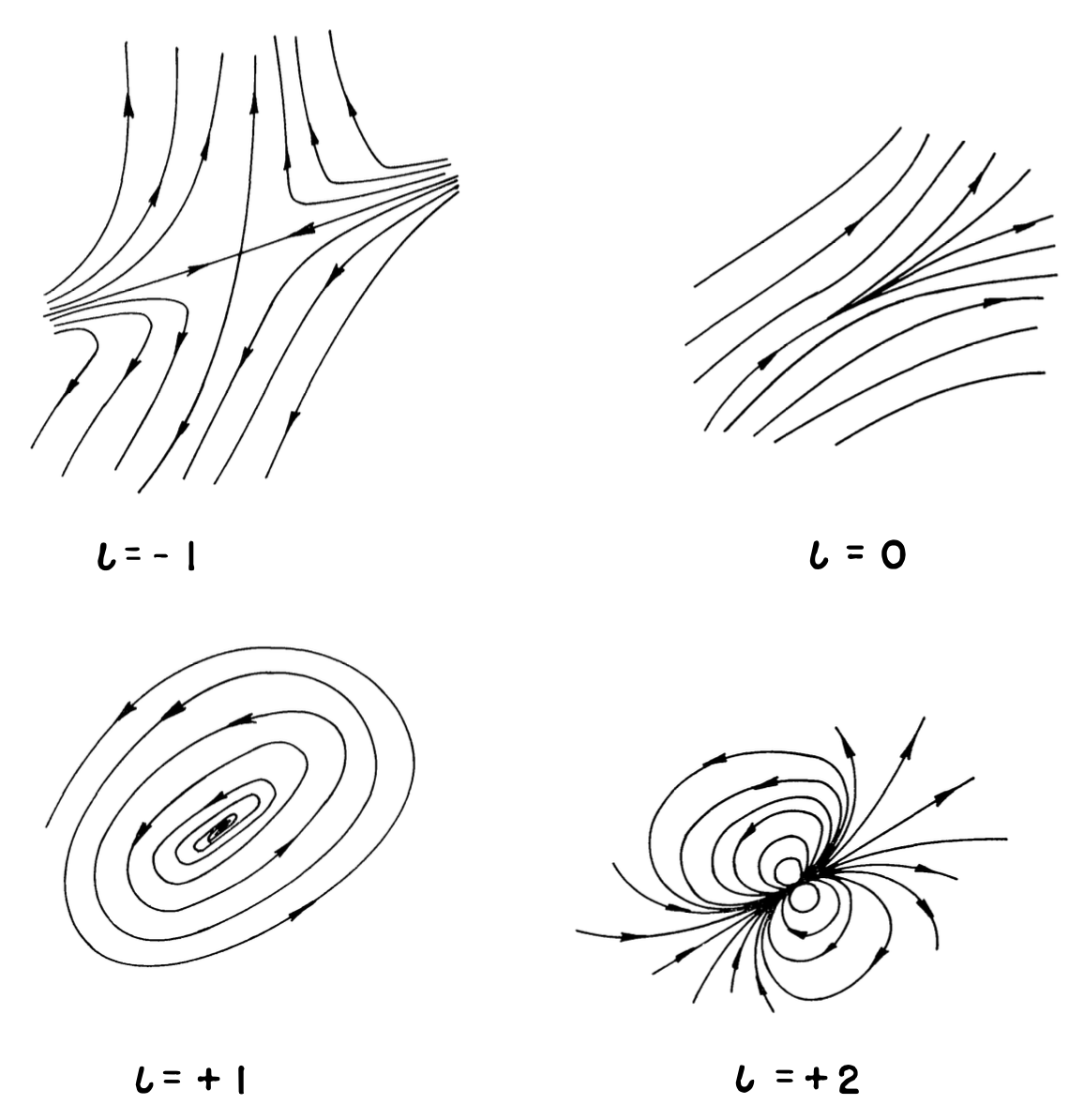
Pero bueno, podría preguntarse, querido lector, ¿qué tiene que ver todo esto con los huracanes? Pues bueno, uno podría imaginar que el viento (es decir, la velocidad del aire) es un campo vectorial sobre la superficie de la Tierra (una 2-esfera). Es natural asumir que este campo se comporta continuamente sobre la Tierra. Entonces, el TBP establece que en este momento (sí, en este preciso momento en el que usted está leyendo) en algún lugar en la Tierra la velocidad del aire es cero. Un lugar como este sería, por ejemplo, el ojo de un huracán.

La figura siguiente muestra las corrientes de aire sobre la superficie de la Tierra en el preciso instante en el que este artículo está siendo escrito. Como puede comprobar, al parecer hay varios huracanes formándose en el hemisferio sur. Lo invito a que compruebe por cuenta propia el Teorema de la Bola Peluda en el sitio web de donde se obtuvo esta imagen.

Resultados de homología singular

Una advertencia.

En esta sección y las siguientes se discuten aspectos más técnicos sobre este teorema. Fueron escritas con el propósito para que el autor no olvide las ideas generales de la demostración del TBP. Un lector no interesado en estos aspectos puede omitir su lectura.

Para demostrar este teorema, necesitamos enunciar cierta maquinaria homológica. Algunos resultados se presentan sin demostración. Para más detalles, ver [1].

Sea $X$ un espacio topológico. Denotemos por $C_p(X)$ al grupo singular de cadenas de dimensión $n$. A los elementos de $C_p(X)$ se les llama p-cadenas singulares en $X$. Existe un homomorfismo de grupos $\partial: C_p(X) \rightarrow C_{p-1}(X)$ llamado operador frontera que satisface que $\partial (\partial c) = 0$ para toda c cadena singular.

El conjunto $Z_p = \ker \partial$ se le conoce como el grupo de p-ciclos, mientras que al conjunto $B_p = Im \partial$ se le conoce como el grupo de (p+1)-fronteras. Debido a la identidad $\partial(\partial c) = 0$ , el grupo $B_p(X)$ es un subgrupo de $Z_p(X)$. Consecuentemente, el p-ésimo grupo de homología, denotado como $H_p(X)$, se define como el cociente de $H_p(X) = Z_p(X) / B_p(X) $.

Si $f: X \rightarrow Y$ es un mapeo continuo entre espacios topológicos, entonces $f$ induce un homomorfismo de grupos $f_\ast: H_p(X) \rightarrow H_p(Y)$ que satisface las siguientes propiedades functoriales:

1. Si $f: X \rightarrow X$ es la identidad, entonces $f_\ast: H_p(X) \rightarrow H_p(X)$ es el homomorfismo identidad.
2. Si $f: X \rightarrow Y $ y $g: Y \rightarrow Z$ son mapeos continuos entre espacios topológicos, entonces $ (g \circ f) \ast = g_\ast \circ f_\ast: H_p(X) \rightarrow H_p(Z)$.

Como consecuencia inmediata de lo anterior, se deduce que si $f: X \rightarrow Y$ es un homeomorfismo, entonces $f_\ast: H_p(X) \rightarrow H_p(Y)$ es un isomorfismo de grupos. Por otro lado, si $A \subset X$ es un retracto de $X$, entonces para toda $p$, el homomorfismo $H_p(A) \rightarrow H_p(X)$ inducido por la inclusión es inyectivo.

Un argumento directo muestra que, $H_0(X)$ es un grupo abeliano libre cuya base consiste en un punto arbitrario por cada componente conexa de $X$.

El siguiente resultado establece una relación entre equivalencia homotópica y homología.

Teorema 1. Si $f, g: X \rightarrow Y$ son mapeos homotópicos, entonces para toda $p \geq 0$, los homomorfismos inducidos $f_\ast, g_\ast: H_p(X) \rightarrow H_p(Y)$ son iguales.

Como consecuencia inmediata se tiene que si $f: X \rightarrow Y$ es una equivalencia homotópica, entonces para toda $p\geq 0$, $f_\ast: H_p(X) \rightarrow H_p(Y)$ es un isomorfismo. En particular, si $X$ es contraible, entonces $H_p(X) = 0$ para toda $p > 0$.

Existe una relación sencilla entre el grupo fundamental $\pi_1(X, x_0)$ de un espacio $X$ y su primer grupo de homología $H_1(X)$: el primer grupo de homología de $X$ es la abelianización del grupo fundamental de $X$.

Consecuentemente, dado que $\pi_1(S^1, 1) \cong \mathbb Z$, se tiene que $H_1(S^1) \cong \mathbb Z$ y $H_1(S^n) \cong 0$ si $n \geq 2$.

El siguiente teorema nos permite calcular grupos de homología de un espacio $X$ mediante el cálculo de grupos de homología de subconjuntos abiertos de $X$. Claro, esta reducción es útil si calcular los grupos de homología de estos abiertos es una tarea más sencilla que calcular los grupos de homología de $X$. Veremos que este es el caso para las n-esferas.

Teorema 2 (Mayer-Vietoris). Sea $X$ un espacio topológico y sean $U, V$ subconjuntos abiertos de $X$ cuya unión es $X$. Entonces, para cada $p$ existe un homomorfismo $\partial_\ast: H_p(X) \rightarrow H_{p-1}(U \cap V)$ tal que la siguiente sucesión es exacta:

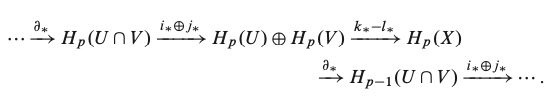
Homología de la n-esfera y teoría de grado

Con los resultados de la sección anterior estamos listos para calcular los grupos de homología de la n-esfera.

Teorema 3. Para $n \geq 1$, $S^n$ tiene los siguientes grupos de homología:

\[H_p(S^n) \cong \begin{cases} \mathbb Z & \text{ si } p=0,\\ 0 & \text{ si } 0 < p < n,\\ \mathbb Z & \text{ si } p=n, \\ 0 & \text{ si } p > n. \end{cases}\]

Demostración. Sean $p_N$ y $p_S$ el polo norte y sur de $S^n$ respectivamente y sean $U = S^n - {p_N}$, $V = S^n - {p_S}$. Entonces, por Mayer-Vietores se obtiene la sucesión exacta

\[H_p(U) \oplus H_p(V) \rightarrow H_p(S^n) \rightarrow H_{p-1}(U\cap V) \rightarrow H_{p-1}(U) \oplus H_{p-1}(V).\]

Dado que $U$ y $V$ son contraibles, si $p > 1$ se tiene que

\[0 \rightarrow H_p(S^n) \rightarrow H_{p-1}(U \cap V) \rightarrow 0,\]

lo cual demuestra que $\partial_\ast$ es un isomorfismo. Dado que $U \cap V$ es homotópicamente equivalente a $S^{n-1}$, tenemos que $H_p(S^n) \cong H_{p-1}(S^{n-1})$ para $p>1$, $n \geq 1$.

Probaremos el resultado mediante inducción sobre $n$. En la sección anterior se mostró que $H_0(S^1) \cong H_1(S^1) \cong \mathbb{Z}$. Además, $H_p(S^1) \cong H_{p-1}(S^0) $ = 0 para $p > 1$, ya que $S^0$ consta de dos componentes conexas con un solo punto.

Suponga que el resultado es cierto para la esfera $S^{n-1}$. Por los resultados de la sección anterior, $H_0(S^n) = \mathbb Z$ y $H_1(S^n) = 0$. Para $p > 1$, la hipótesis de inducción establece que

\[H_{p-1}(S^{n-1}) \cong \begin{cases} \mathbb Z & \text{ si } p=0,\\ 0 & \text{ si } 0 < p-1 < n-1,\\ \mathbb Z & \text{ si } p-1=n-1, \\ 0 & \text{ si } p > n-1. \end{cases}\]

Pero $H_p(S^n) \cong H_{p-1}(S^{n-1})$, lo que completa la demotración.

A grosso modo, la homología sólo nos da información acerca de la $n-$esfera cuando $p = n$.

Suponga que $n \geq 1$. Por el Teorema 3, $H_n(S^n)$ es un grupo cíclico infinito. Si $f: S^n \rightarrow S^n$ es un mapeo continuo, entonces $f$ induce un homomorfismo $f_\ast: H_n(S^n) \rightarrow H_n(S^n)$ de grupos. Todo homomorfismo entre grupos cíclicos es de la forma $g \mapsto g^m$ para algún entero fijo $m$. El entero $m$ que satisface esta propiedad para $f_\ast$ se le llama el grado de $f$ y se denota por $deg(f).$ En particular, para el caso $n=1$, al grado de $f: S^1 \rightarrow S^1$ se le llama número de enrollamiento de $f$. El grado es una generalización de este concepto para $n-$esferas con $n > 1$.

Como consecuencia inmediata de las propiedades functoriales de la homología se tiene el siguiente resultado. Suponga que $n\geq1$ y $f,g : S^n \rightarrow S^n$ son mapeos continuos. Entonces

1. $deg(g \circ f) = (deg(g)) \cdot (deg(f))$.
2. Si $f$ y $g$ son homotópicos, entonces $deg(f) = deg(g)$.

Cabe resaltar que el converso del punto 2. de la proposición también es cierto. Por tanto, el grado nos ofrece una clasificación homotópica de mapeos de $S^n$ en $S^n$.

Si $Id_{S^n}: S^n \rightarrow S^n$ es el mapeo identidad, entonces su grado es igual a $1$. Esto muestra que $Id_{S^n}$ no es homotópicamente nula . Sea $\alpha: S^n \rightarrow S^n$ el mapeo antipodal $x \mapsto -x$. Su grado es igual a $(-1)^{n+1}$. Por tanto, $\alpha$ es homotópico a la identidad si y solo si $n$ es impar.

Resultado principal

Un campo vectorial en $S^n$ es un mapeo continuo $S^n \rightarrow \mathbb R^{n+1}$ tal que para toda $x \in S^n$, $V(x)$ es tangente a $S^n$ en $x$. Esto es, $V(x) \cdot x = 0$ para toda $x \in S^n$.

Con lo anterior, estamos listos para demostrar el teorema de la bola peluda que enuciaremos de nuevo como recordatorio.

Teorema. Existe un campo vectorial en $S^n$ que no se anula en ningún punto si y solo si $n$ es impar.

Demostración. Supóngase que existiera tal campo vectorial $V$. Podemos asumir que $\lvert V(x) \rvert = 1$ (hágase $V(x) / \lvert V(x) \rvert$) para toda $x \in S^n$. La función $H: S^n \times I \rightarrow S^n$ definida como

\[H(x, t) = (cos \ \pi t)x + (sen \ \pi t) V(x)\]

es una homotopía entre el mapeo antipodal $\alpha $ y la identidad. Por un resultado de la sección anterior, esto ocurre si y solo si $n$ es impar.

Conversamente, suponga que $n = 2k-1$ es impar. Un argumento directo muestra que el mapeo $V: S^n \rightarrow \mathbb R^{n+1}$ definido como

\[V(x_1, \ldots, x_{2k}) = (x_2, -x_1, x_4, -x_3, \ldots, x_{2k}, -x_{2k-1})\]

es un campo vectorial que no se anula en ningún punto $x \in S^n$.

Cabe mencionar que la maquinaria desarrollada hasta ahora nos permite demostrar otros teoremas interesantes. Esto lo discutiremos en notas posteriores.

Referencias

[1] Lee, J. (2010). Introduction to Topological Manifolds. Springer New York.

[2] Milnor, John W. (1997). Topology from the differentiable viewpoint. Princeton Landmarks in Mathematics. Princeton, NJ: Princeton University Press. ISBN 0-691-04833-9.